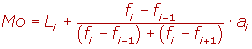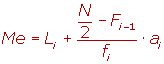Coeficiente de correlación de Pearson

Coeficiente de correlación de Pearson

Es una medida de la relación lineal entre dos variables aleatorias cuantitativas. A diferencia de la covarianza, la correlación de Pearson es independiente de la escala de medida de las variables.

De manera menos formal, podemos definir el coeficiente de correlación de Pearson como un índice que puede utilizarse para medir el grado de relación de dos variables siempre y cuando ambas sean cuantitativas.

1- En una tarea de clasificación de patrones que constaba de 10 láminas se obtuvieron los

siguientes datos de las diferencias de las distancias logarítmicas del estímulo a clasificar con

respecto a los prototipos de las dos clases en que podía ser encuadrado y del número de

errores cometidos por los sujetos:

 Lámina 1 2 3 4 5 6 7 8 9 10

Diferencia 0,71 0,67 1,98 1,61 0,67 1,48 0,25 1,44 1,06 0,95

Nº errores 12 10 4 2 6 5 16 3 4 8

a) Calcule el coeficiente de correlación de Pearson e interprete el resultado.

El coeficiente de correlación será:

r= 0 829

RECTA DE REGRESION

La recta de regresión es la que mejor se ajusta a la nube de puntos.

La recta de regresión pasa por el punto  llamado centro de gravedad.

Recta de regresión de Y sobre X

La recta de regresión de Y sobre X se utiliza para estimar los valores de la Y a partir de los de la X.

La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable X.

Recta de regresión de X sobre Y

La recta de regresión de X sobre Y se utiliza para estimar los valores de la X a partir de los de la Y.

La pendiente de la recta es el cociente entre la covarianza y la varianza de la variable Y.

Si la correlación es nula, r = 0, las rectas de regresión son perpendiculares entre sí, y sus eucaciones son:

y = 

x =  

Las notas de 12 alumnos de una clase en Matemáticas y Física son las siguientes:

Matemáticas	2	3	4	4	5	6	6	7	7	8	10	10
Física	1	3	2	4	4	4	6	4	6	7	9	10

Hallar las rectas de regresión y representarlas.

xi	yi	xi ·yi	xi2	yi2
2	1	2	4	1
3	3	9	9	9
4	2	8	16	4
4	4	16	16	16
5	4	20	25	16
6	4	24	36	16
6	6	36	36	36
7	4	28	49	16
7	6	42	49	36
8	7	56	64	49
10	9	90	100	81
10	10	100	100	100
72	60	431	504	380

1º Hallamos las medias ariméticas.

2º Calculamos la covarianza.

3º Calculamos las varianzas.

4ºRecta de regresión de Y sobre X.

4ºRecta de regresión de X sobre Y.

Medidas de tendencia central

Medidas de tendencia central:

Moda

La moda es el valor que tiene mayor frecuencia absoluta.Se representa por M_o.Se puede hallar la moda para variables cualitativas y cuantitativas.

Mediana

Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. La mediana se representa por M_e.La mediana se puede hallar sólo para variables cuantitativas.

Media aritmética

La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.

MODELOS MATEMÁTICOS:

(DATOS AGRUPADOS)

MODA:  

MEDIANA: 

MEDIA ARITMÉTICA 

(DATOS NO AGRUPADOS)

MEDIA: 

MEDIANA:

Mediana =X_[(n/2)+1/2]

_{MEDIA PONDERADA:}

EJEMPLO

En matemáticas, un alumno tiene las siguientes notas:  4, 7, 7, 2, 5, 3

n = 6 (número total de datos)

La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.

Ejemplo 2:

Cuando se tienen muchos datos es más conveniente agruparlos en una tabla de frecuencias y luego calcular la media aritmética. El siguiente cuadro con las medidas de 63 varas de pino lo ilustra.

Largo (en m)	Frecuencia absoluta	Largo por Frecuencia absoluta
5	10	5          .       10  =   50
6	15	6          .        15 =   90
7	20	7          .        20 =  140
8	12	8          .        12 =    96
9	6	9            .          6 = 54
	Frecuencia total = 63	430

Se debe recordar que la frecuencia absoluta indica cuántas veces se repite cada valor, por lo tanto, la tabla es una manera más corta de anotar los datos (si la frecuencia absoluta es 10, significa que el valor a que corresponde se repite 10 veces).

Moda (Mo)

Es la medida que indica cual dato tiene la mayor frecuencia en un conjunto de datos; o sea, cual se repite más.

Ejemplo 1:

Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.

                  5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3

La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)

Ejemplo 2:

               20, 12, 14, 23, 78, 56, 96

En este conjunto de datos no existe ningún valor que se repita, por lo tanto, este conjunto de valores no tiene moda.

Mediana (Med)

Para reconocer la mediana, es necesario tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide el total de casos (N) entre dos, y el valor resultante corresponde al número del caso que representa la mediana de la distribución.

Es el valor central de un conjunto de valores ordenados en forma creciente o decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.

Según el número de valores que se tengan se pueden presentar dos casos:

Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.

Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).

Ejemplo 1:

Se tienen los siguientes datos:  5, 4, 8, 10, 9, 1, 2

Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene:  1, 2, 4,  5, 8, 9, 10

El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares.

Ejemplo 2: 

El siguiente conjunto de datos está ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de valores pares, por lo tanto, la Med será el promedio de los valores centrales.

     21, 19, 18, 15,  13, 11, 10, 9, 5, 3

          

Ejemplo 3:

                  

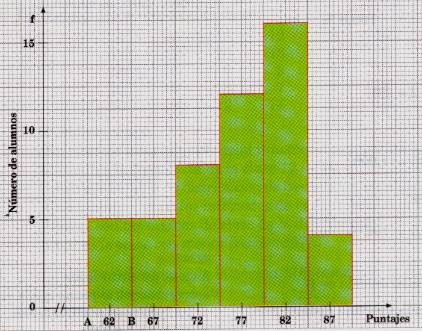
Interpretando el gráfico de barras podemos deducir que:

 5 alumnos obtienen puntaje de 62

5 alumnos obtienen puntaje de 67

8 alumnos obtienen puntaje de 72

12 alumnos obtienen puntaje de 77

16 alumnos obtienen puntaje de 82

4 alumnos obtienen puntaje de 87

lo que hace un total de 50 alumnos

Sabemos que la mediana se obtiene haciendo

 lo cual significa que la mediana se ubica en la posición intermedia entre los alumnos 25 y 26 (cuyo promedio es 25,5), lo cual vemos en el siguiente cuadro:

puntaje	alumnos
62	1
62	2
62	3
62	4
62	5
67	6
67	7
67	8
67	9
67	10
72	11
72	12
72	13
72	14
72	15
72	16
72	17
72	18
77	19
77	20
77	21
77	22
77	23
77	24
77	25
77	26
77	27
77	28
77	29
77	30
82	31
82	32
82	33
82	34
82	35
82	36
82	37
82	38
82	39
82	40
82	41
82	42
82	43
82	44
82	45
82	46
87	47
87	48
87	49
87	50

El alumno 25 obtuvo puntaje de 77

El alumno 26  obtuvo puntaje de 77

Entonces, como el total de alumnos es par debemos promediar esos puntajes:

La mediana es 77, lo cual significa que 25 alumnos obtuvieron puntaje desde 77 hacia abajo (alumnos 25 hasta el 1 en el cuadro)  y 25 alumnos obtuvieron puntaje de 77 hacia arriba (alumnos 26 hasta el 50 en el cuadro).

DESVIACIÓN ESTÁNDAR

DESVIACIÓN ESTÁNDAR:

Desviación estándar

La desviación estándar (σ) mide cuánto se separan los datos.

La fórmula es fácil: es la raíz cuadrada de la varianza. Así que, "¿qué es la varianza?"

Varianza

la varianza (que es el cuadrado de la desviación estándar: σ²) se define así:

Es la media de las diferencias con la media elevadas al cuadrado. 

MODELOS MATEMÁTICOS:

VARIANZA

DESVIACIÓN ESTÁNDAR 




EJEMPLO DE VARIANZA 

En un partido de baloncesto, se tiene la siguiente anotación en los jugadores de un equipo: 0,2,4,5,8,10,10,15,38. Calcular la varianza de las puntuaciones de los jugadores del equipo.

Aplicando la fórmula x¯=0+2+4+5+8+10+10+15+389=929=10.22 se obtiene la media.

Seguidamente se aplica la fórmula de la varianza:

σ2=(0−10.22)2+(2−10.22)2+(4−10.22)2+(5−10.22)2+(8−10.22)2+(10−10.22)2+(10−10.22)2+(15−10.22)2+(38−10.22)29==10.222+8.222+6.222+5.222+2.222+0.222+4.782+27.7829==104.4484+67.5684+38.6884+27.2484+4.9284+0.0484+22.8484+771.72849==1037.55569=115.28

EJEMPLO DE DESVIACIÓN ESTÁNDAR 

-El gerente de una empresa de alimentos desea saber que tanto varían los pesos de los empaques (en gramos), de uno de sus productos; por lo que opta por seleccionar al azar cinco unidades de ellos para pesarlos. Los productos tienen los siguientes pesos (490, 500, 510, 515 y 520) gramos respectivamente.

Por lo que su media es:

Con lo que concluiríamos que el peso promedio de los empaques es de 507 gramos, con una tendencia a variar por debajo o por encima de dicho peso en 12 gramos. Esta información le permite al gerente determinar cuanto es el promedio de perdidas causado por el exceso de peso en los empaques y le da las bases para tomar los correctivos necesarios en el proceso de empacado.